【人気ダウンロード！】 prove that (x-y)^3 (y-z)^3 (z-x)^3=3(x-y)(y-z)(z-x) 317936

To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2` If x, y, z are different and Δ = (x, x2, 1 x3), (y, y2, 1 y3), (z, z2, 1 z3) = 0 then show that 1 xyz = 0 We have Now, we know that If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants Click here 👆 to get an answer to your question ️ Solve for (x, y, z) if x y z = 3, x2 y2 z2 = 3, x3 y3 z3 = 3 krishnapohekar6 krishnapohekar6

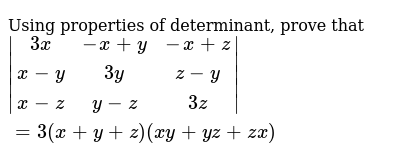
Using Properties Of Determinant Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx

Prove that (x-y)^3 (y-z)^3 (z-x)^3=3(x-y)(y-z)(z-x)

Prove that (x-y)^3 (y-z)^3 (z-x)^3=3(x-y)(y-z)(z-x)- Answer is (xy z)(x^2 y^2 xyz z^2) You can check by multiplying it out Notice that each term is a perfect cube x^3 y^3 = (xy)^3 So we have a sum of cubes, and the factoring formula is a^3 b^3 = (ab)(a^2abb^2) So we use a = xy and b = z to get x^3 y^3 z^3 = (xy)^3 z^3 = ((xy) z)((xy)^2(xy)zz^2) =(xy z)(x^2 y^2 xyz z^2) check by multiplying it out toMathcircler "Previous Answer It depends If you want three Real numbers x ,y , z satisfying x^ 3 y^ 3 z ^3 =33 then there are infinitely many, and they are very easy to find If you want three Ra

यद X Y Z 9 Xy Yz Zx 23 तब X 3 Y 3 Z 3 3xyz Youtube

 Prove that in the expansion of `(1x)^n(1y)^n(1z)^n` , the sum of the coefficients of the terms of degree `ri s^(3n)C_r` A `(""^(n)C_(r))^(3)`Using x = 2, y = 3, and z = 4, evaluate each expression and match to its corresponding answer SW 1 ху 2 A) 6 2 х(у 2) B) 1 3 2z Зу C) 2 4 x yz D) 14 5 ху— хz E) 12 6 2(г— х) F) 1 7 yz X y G) x y 8 What is the value of x 3y z if x = 3, y = 3, and z = 4 1 See answer gheedominique is waiting for your help Add your answer and earn points kphung kphung Substitute the values 33(3)4 First evaluate the multiplication 394 39=12 124=16 Final answer16 New questions in Biology

(((x 3)•(yz))y 3 •(zx))z 3 •(xy) Step 3 Equation at the end of step 3 (x 3 •(yz)y 3 •(zx))z 3 •(xy) Step 4 Trying to factor by pulling out 41 Factoring x 3 yx 3 zxy 3 xz 3 y 3 zyz 3 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 y 3 zxy 3 Group 2 x 3 yx 3 zSolve for z 2/x=3/y1/z 2 x = 3 y 1 z 2 x = 3 y 1 z Rewrite the equation as 3 y 1 z = 2 x 3 y 1 z = 2 x 3 y 1 z = 2 x 3 y 1 z = 2 x Subtract 3 y 3 y from both sides of the equation 1 z = 2 x − 3 y 1 z = 2 x 3 y Find the LCD of the terms in the equation Tap for more steps` X ` Y Z =` 33X ` ` ` Z = 5 ` X 2Y Z =` 3 ` Here are the seven steps 1 Pick a letter (If one of the equations has only two letters, choose the ` `letter that is missing) 2 Pick an equation that contains that letter 3 Solve for that letter in that equation 4 Substitute what you get into any other equations that contains that

 2^x 3^y = z^2 1 where x, y, and z are nonnegative integers We can see that 1 is a congruence modulo 8 3^y = z^2 (mod 8) 2 When z=1 and and y=2 we have 3^2 = 1 (mod 8) 3 and by Fermat's theorem So this means that y must be even As y is even, we can write y = 2k for some integer k Move all terms containing x to the left, all other terms to the right Add '1yz' to each side of the equation xy xz yz 1yz = t 1yz Combine like terms yz 1yz = 0 xy xz 0 = t 1yz xy xz = t 1yz Reorder the terms 1t xy xz yz = t 1yz 1t yz Reorder the terms 1t xy xz yz = t 1t 1yz yz CombineUsing Formula, a^3 b^3 c^3 3abc = (a b c)(a^2 b^2 c^2 ab ac bc) Adding 3abc both side a^3 b^3 c^3 = (a b c)(a^2 b^2 c^2 ab ac bc

X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In

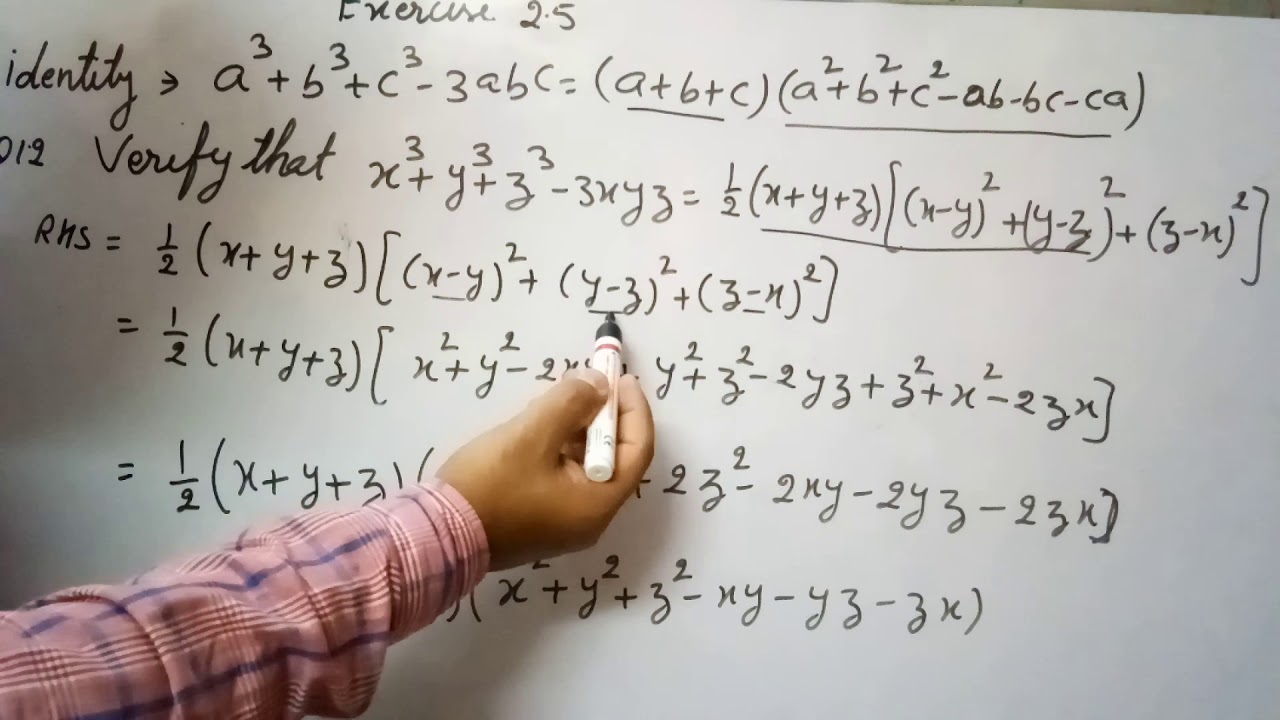
Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube

 Click here 👆 to get an answer to your question ️ prove that (xy)³(yz)³(zx)³3(xy)(yz)(zy)=2(x³y³z³3xyz) The answer is z=3(axy) Beginning Equation a=xyz/3 First multiply both sides of the equation by 3 3a=3x3yz Subract 3x and 3y from both sides 3a3x3y=z Factor out the 3 3(axy)=z Show that $$(xy)^3(yz)^3(zx)^3 = 3(xy)(yz)(zx)$$ This can be shown through expansion but there is a more elegant solution I cannot discover anything I would consider elegant Can anyone h

Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5

Partial Differentiation If U F Y Z Z X X Y Prove That әu әx әu әy әu әz 0 Youtube

 To evaluate the expression, substitute the given values for x, y and z into it The expression can be simplified by collecting like terms #rArr2x^32y^2z^4#3*3x2*y*4z*x*y*z This deals with simplification or other simple results Overview Steps Topics Terms and topics Links Related links 1 solution (s) found (3^2*2^2x^3y^2z^2)Click here👆to get an answer to your question ️ If x y z = 0 , then x^3 y^3 z^3 =

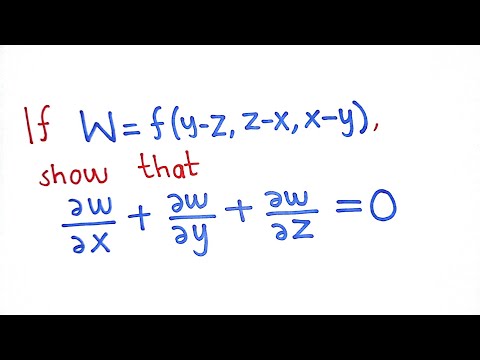
If W F Y Z Z X X Y Show That Dw Dx Dw Dy Dw Dz 0 Youtube

2

 (xy)^3 (yz)3 (zx)^3 >= 3(xy)(yz)(zx) But that is not the question set Please note that this is the first chapter and all that has been covered is basic number theory, rational powers, inequalities and divisibility I am assuming those are the only tools I have at my disposal, I have not been introduced to any identities etcY=xz/3 Simple and best practice solution for y=xz/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it prove that (xy)3(yz)3(zx)33(xy) (yz) (zx) =2(x3y3 z 3 3xyz) Maths Polynomials Using identity a 3 b 3 c 3 3abc = (abc)(a 2 b 2 c 2 ab

If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____No integers x;y;z with xyz6= 0 satisfy x3 y3 z3 = 0 Proof We may assume that x, y, and zare pairwise coprime If xyzis not divisible by 3, then the equation has no solution even in Z=(9), where every nonzero cube is 1 Suppose then, without loss of generality, that 3jz We will work in the UFD R= Z with = ( 1i p 3)=2, a root of theThere are infinite solutions as you have 3 variables but only one equation However, it is interesting to note that there is no solution for which all of the varibles x,y,z are integersFermat's last theorem says that there is no solution of x^n

If X Y Z 6 And Xy Yz Zx 12 Then Show That X3 Y3 Z3 3xyz Maths Polynomials 12 Meritnation Com

The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1 Youtube

(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xySimple and best practice solution for Z=3xy equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,On x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uv

New Question Verify That X3 Y3 Z3 3xyx 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Tex Textless H2 Brainly In

If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora

A classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, mathx^3 y^3 zFind 3x2 y3 y3 z if x = 3, y = 2, and z = 5 1298Complete cubic parametrization of the Fermat cubic surface w 3 x 3 y 3 z 3 = 0 This is a famous Diophantine problem, to which Dickson's History of the Theory of Numbers, Vol II devotes many pages It is usually phrased as w 3 x 3 y 3 =z 3 or w 3 x 3 =y 3 z 3, with the implication that the variables are to be positive, as in the integer solutions 3 3 4 3 5 3 =6 3 (an amusing

Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In

Class 9

Solve for y z=((xy)/3)w Rewrite the equation as Combine and Divide each term by and simplify Tap for more steps Divide each term in by Simplify Tap for more steps Multiply the numerator by the reciprocal of the denominator Cancel the common factor ofFactor (yz)^38 (y z)3 − 8 ( y z) 3 8 Rewrite 8 8 as 23 2 3 (yz)3 −23 ( y z) 3 2 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = yz a = y z and b = 2 b = 2 (yz− 2)((yz)2 (yz)⋅2 22) ( y z 2Solution for If x* = y" = z*, prove that 3,3 log, x, 3log, y,7 log, z from an AP 18 %3D 12 „18

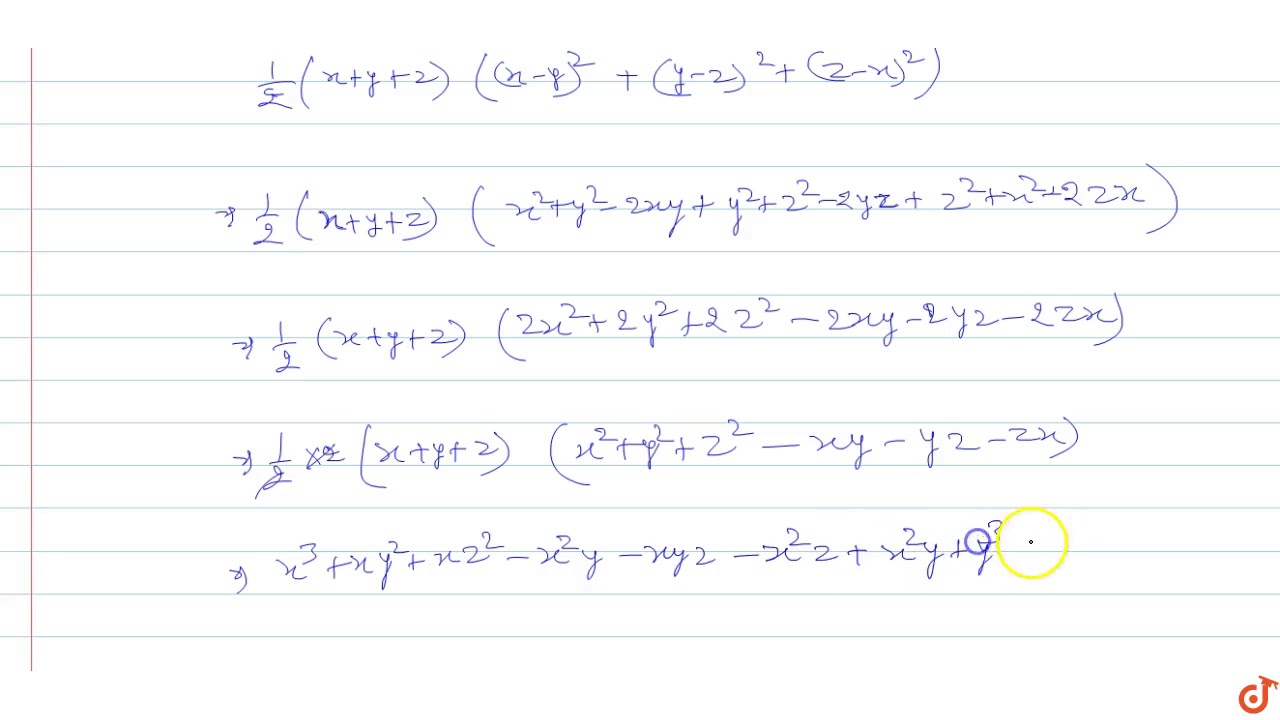
Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube

Using Properties Of Determinant Prove That 1 X Y X 2 Y 2 1 Y Z Y 2 Z 2 1 Z X Z 2 X 2 X Y Y Z Z X

 What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?Please refer to Alon Amit, PhD in Mathematics; First, Schur's inequality provides that $$ x^3y^3z^33xyz\ge xy(xy)yz(yz)zx(zx) $$ Then, $$ xy(xy)\ge 2xy\sqrt{xy} $$ and hence $$ x^3y^3z^33xyz\ge 2\big(xy\sqrt{xy} yz\sqrt{yz} zx\sqrt{zx} \big) $$

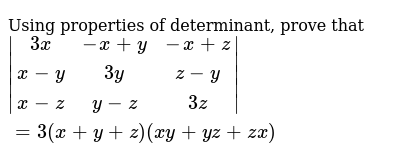
Using Properties Of Determinant Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx

Pdf Extrema Of Xy Yz Zx When X Y Z And Xyz Are Constant

Find x^1/3 y^1/3 z^1/3 = 0 Then find (x y z)^3 Hello Student Thanks & Regards Arun Kumar Btech, IIT Delhi Askiitians FacultyMathematical Proofs (4th Edition) Edit edition Problem 4E from Chapter 4 Let x, y ∈ Z Prove that if 3 x and 3 y, then 3 (x2 − y2) Get solutions Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro

If X Y Y Z Then Simplify Xyz X Y Z 3 Xy Yz Zx 3 Youtube

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Xz Youtube

Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2x3yz=2;x5y5z=3;3xy3z=5 Tiger Algebra SolverI don't know what you really want to ask , but here is at least a bit of content to this for this formula Since it is homogenous in x,y,z (so all terms have equal degree), you can read it as a description of a object of algebraic geometry eitherIf 3x=4y=12zthen prove that xyz=xy 3^x = 4^y = 12^z take 3^x = 12^z 3 = 12^zx1 take 4^y =12^z 4 = 12^zy2 multiply equation 1 and 2 you get 12 =12^zx zy

Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In

Www Nextgurukul In Questions Answers Forum Question Academic Prove X3 Y3 Z3 3xyz X Y Z X Y2

You can put this solution on YOUR website!

If Log X Y Z Logy Z X Logz X Y Then Prove That X X Y Y Z Z 1

If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora

X Y Xy 3 Y Z Yz 8 And Z X Zx 15 What Is The Value Of 6xyz Brainly In

How To Factorize X Y Y Z Z X Quora

How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo

Example 32 Show That Determinant 2xyz X Y Z 3 Class 12

Show That The Functions U X Y Z V Xy Yz Zx And W X 3 Y 3 Z 3 3xyz Are Independent And Find The Relation Between Them Mathematics

Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In

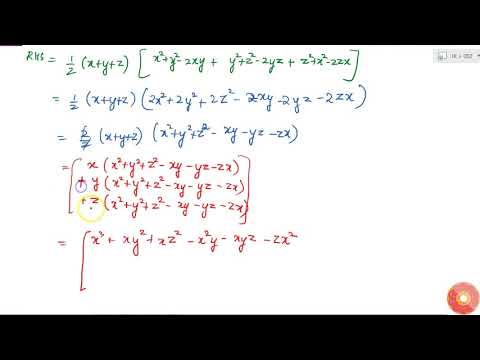
Verify That X 3 Y 3 Z 3 3x Y Z 1

Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z

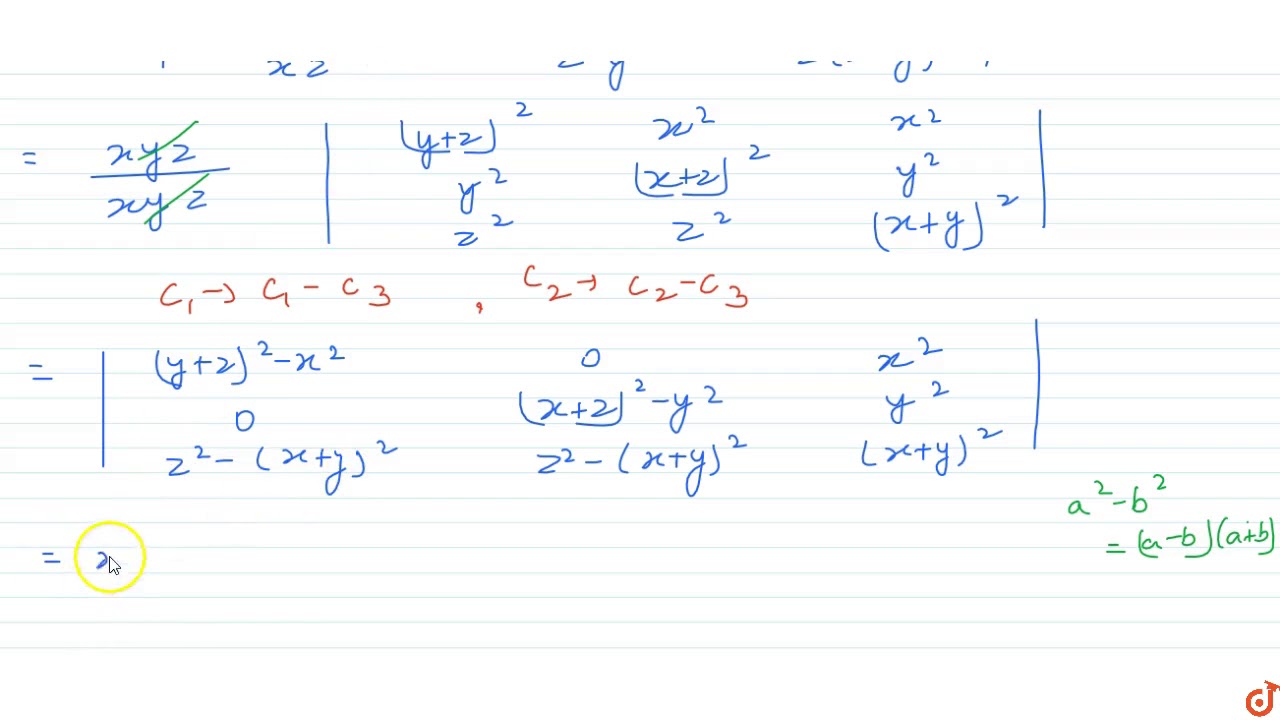
Prove That Y Z 2 Xy Zx Xy X Z 2 Yz Xz Zy X Y 2 Xyz X Y Z 3 Youtube

If X 2 Y 2 Z 2 1 Then Xy Yz Zx Lies In

Without Finding The Cubes Factorise X Y Y Z Z X Brainly In

Using Properties Of Determinant Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx

Using Properties O Determinants Prove That 1 X X 3 1 Y Y 3 1 Z Z 3 Sarthaks Econnect Largest Online Education Community

Show That For All Real Numbers X Y Z Such That X Y Z 0 And Xy Yz Zx 3 Sarthaks Econnect Largest Online Education Community

Using Properties Of Determinant Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3 Youtube

The Value Of X Y 3 Y Z 3 Z X 3 X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Is B 1 C 2 X Y Z 1 D X Y Y Z Z X 1

The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Brainly In

If X Y Z Are Real Numbers If X Y Z 13 X Y Z 1 And X Y Z 1 What Is The Value Of Xy Yz Zx Quora

If Cos Y Z Cos Z X Cos X Y 3 2 Prove That Cos X Cos Y Cos Z 0 Sin X Siny Sin

यद X Y Z 9 Xy Yz Zx 23 तब X 3 Y 3 Z 3 3xyz Youtube

If Cos Y Z Cos Z X Cos X Y 3 2 Prove That Cos X Cos Y Cos Z 0 Sin X Siny S Youtube

How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube

Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community

If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube

Prove That 2x 3 2y 3 2z 3 6xyz X Y Z X Y 2 Y Z 2 Z X 2 Brainly In

Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community

Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Maths Polynomials Meritnation Com

Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In

Prove That X Y Cube Y Z Cube Z X Cube 3 X Y Y Z Z X 2 Xcube Ycube Zcube 3xyz Brainly In

X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3 Youtube

2

Some Strong Sufficient Conditions For Cyclic Homogeneous Polynomial Inequalities Of Degree Four In Nonnegative Variables Pdf Free Download

Www M A Org Uk Resources Symmetryplus answers76 Pdf

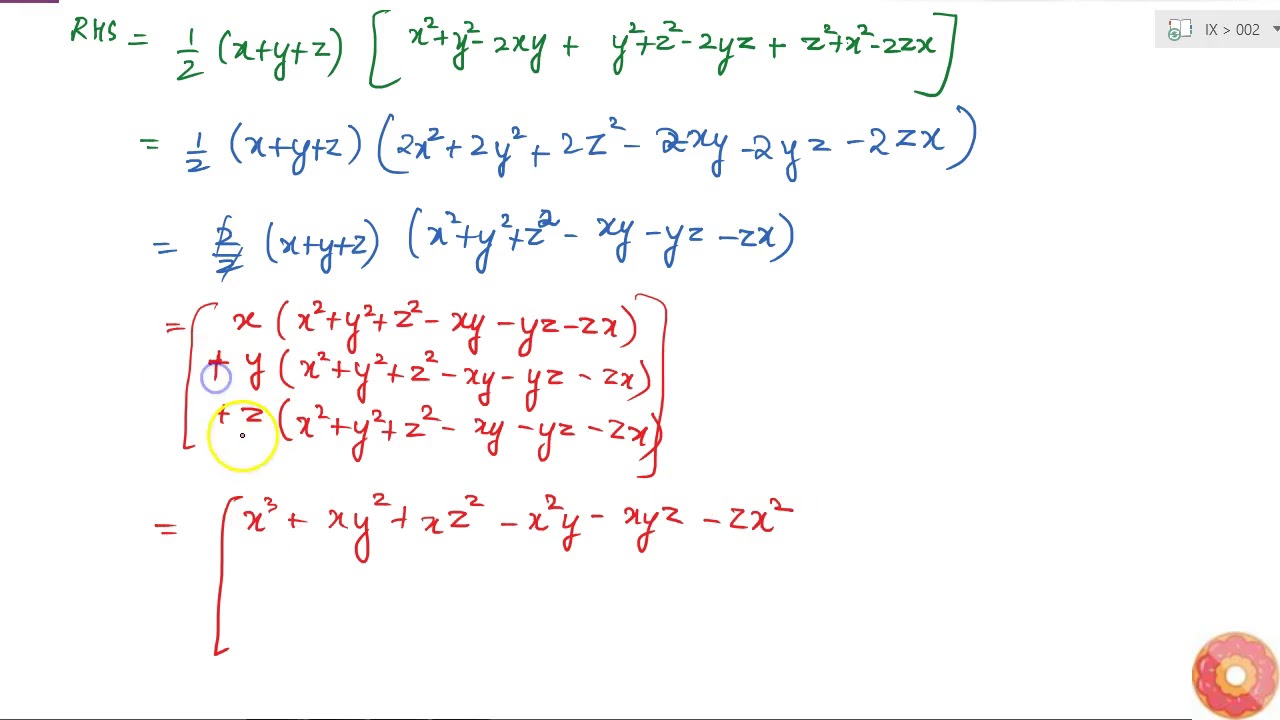
Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube

26 Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Maths Polynomials Meritnation Com

Factorise 2x Y Z 3 2y Z X 3 2z X Y 3

Using Properties Of Determinants Prove That C C C1 1 1 3 X 1 3 Y 1 1 1 1 3 Z 1 9 3 X Y Z X Y Y Z Z X

If X Y Z 19 Xyz 216 And Xy Yz Zx 114 Then The Value Of X 3 Y 3 Z 3 Xyz Is The Math Guru

How Can We Prove That For Xy Z 10 Yz X 14 Zx Y 11 Here X 2 Y 3 Z 4 Quora

Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In

If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube

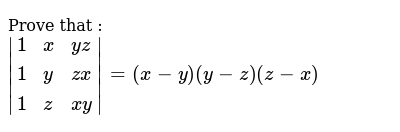
Find The Value Of 1 X Yz 1 Y Zx 1 Z Xy

X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55

Using Properties Of Determinants Prove The Following 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Xz

Factorize X Y 3 Y Z 3 Z X 3 Youtube

Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx

Using Properties Of Determinants Prove The Following X X 2 1 Px 3 Y Y 2 1 Py 3 Z Z 2 1 Pz 3 1 Pxyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community

Example 32 Show That Determinant 2xyz X Y Z 3 Class 12

Prove That 2x3 2y3 2z3 6xyz X Y Z X Y 2 Y Z 2 Z X 2 Hence Evaluate 2 7 3 2 9 3 2 13 3 6 7 9 13 Mathematics Topperlearning Com V780o2jj

Using Properties Of Determinants Prove That Y X 2 Xy Zx Xy X Z 2 Yz Xz Yz X Y 2 2xyz X Y Z 3 Sarthaks Econnect Largest Online Education Community

Factorise 2x Y Z 3 2y Z X 3 2z X Y 3

Using The Properties Deteminants 3x X Y X Z X Y 3y Z Y X Z Y Z 3z Studyrankersonline

2

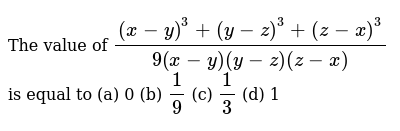
The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1

The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1

Www Topperlearning Com Answer Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers 3gc3fduu

Find The Value Of 1 X Yz 1 Y Zx 1 Z Xy

Find The Value Of X Y Y Z Z X Brainly In

X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3 Youtube

Q 10 Show That The Expression X 2 Yz 3 Y 2 Zx 3 Z 2 Xy 3 3 X 2 Yz Y 2 Zx Z 2 Xy Is Youtube

Royalsocietypublishing Org Doi Pdf 10 1098 Rstl 1865 0014

Factorise 2x Y Z 3 2y Z X 3 2z X Y 3

Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community

X Y Z 3 Y Z X 3 Z X Y 3 X Y Z 3 24xyz Mathematics Stack Exchange

Factorise X Y 3 Y Z 3 Z X 3 Brainly In

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

X2 Y2 3 Y2 Z2 3 Z2 X2 3 2 23 2 23 53 3 X Y Scholr

Using Properties Of Determinants Prove That Y X 2 Xy Zx Xy X Z 2 Yz Xz Yz X Y 2 2xyz X Y Z 3 Sarthaks Econnect Largest Online Education Community

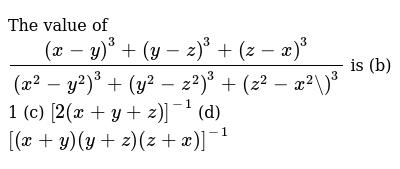
The Value Of X Y 3 Y Z 3 Z X 3 X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Is B 1 C 2 X Y Z 1 D X Y Y Z Z X 1

If 2 X 3 Y 12 Z Then Prove That Xy Z X 2y Mathematics Topperlearning Com 8v1liiww

Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube

If Xy 3 Yz 6 Zx 2 Find X Y Z Brainly In

Ex 4 4 4 Using Cofactors Of Elements Of Third Column Evaluate

Prove That X3 Y3 Z3 3xy X Y Z X2 Y2 Z2 Xy Yz Zx Only By Lhs Brainly In